회귀 소개
회귀 분석은 Y = Wx+b 라는 직선(모델)에서 X는 특성(feature)이며 y는 label이다. 이 Y = Wx+b 직선의 X를 넣었을 때 나오는 값을 Y^이라고 하면 label인 Y와 직선에서 나온 예측값의 최소를 구하는 W,b을 설정해주는것이 Linear Rregession에 핵심이다.
그렇다면 x1,x2,x3.... , y1,y2,y3.... 데이터가 있을 때 이것을 제곱 평균식으로 나타내면 다음과 같다.

n은 데이터의 갯수이며 loss는 손실함수이다.
이때 loss의 y^을 Wx+b로 표현할 수 있다. 표현한 식은 다음과 같다.

이 loss의 값이 최소가 되게 하는 것이 Linear Regression이다. 그렇다면 x값과 y의 값은 데이터에서 주어지므로 결론적으로는 w,b의 값을 미분하여 경사하강법을 이용하여 w업데이트하면 된다. b값도 마찬가지로 경사하강법을 이용하여 업데이트하면된다.
y축을 loss로 하고 x축을 w로 한 그래프를 그리면 2차함수 그래프가 나오는데 2차함수에서 최소값은 미분해서 기울기가 최소인점이므로 미분해서 기울기가 최소인 W를 구하면 y축이 loss값이므로 loss값의 최소값을 구하게되는 것이다.
손실함수를 w로 미분한 식은 다음과 같다.

손실함수를 b로 미분한 식은 다음과 같다.
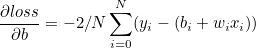
또 손실함수 그래프에서 기울기가 -이면 더해주고 +이면 감소시켜야되는 원리를 이용하여 식을 정리하면

위와 같은 식을 만들 수 있다. 여기서 a는 learning rate라고 w를 증가시켜주는 비율이다.
이제 위에서 만들어준 식들을 바탕으로 파이썬을 이용하여 코드를 작성해 보겠다.
파이썬 실습
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline일단 필요한 라이브러리를 import 해주었다.
# y = 4x+6을 예측하는 모델
# 테스트 데이터 셋을 만들어 준다.
np.random.seed(0) #동일한 세트의 난수가 나오기위해 사용
x = 2*np.random.rand(100,1) # random.rand: 0~1까지의 표준정규분포 난수 array를 반환한다.
y = 6+4*x+np.random.randn(100,1) #random.randn :평균 0 ,표준편차 1의 가우시간 표준정규분표 난수를 생성 array를 반환
plt.scatter(x,y)y = 4x+6을 예측하는 모델을 만들기 위해 y = 4x+6에서 난수를 주어서 데이터를 만들어 주었다. (Linear Regression은 표준정규분포와 같은 데이터에서 성능이 좋음)
산점도 그래프를 그리면 다음과 같다.

# 실제값과 예상값의 평균을 계산
def get_cost(y,y_pred):
N = len(y)
cost = np.sum(np.square(y-y_pred))/N
return cost그 다음에는 실제값과 예측값을 계산하는 함수를 만들었다.

이 식을 그대로 파이썬 코드로 구현했다.
# w,b을 업데이트할 w_update,b_update 반환
def get_weight_update(w,b,x,y,learning_rate = 0.01):
N = len(y)
# 크기가 각각 w,b와 동일한 크기를 가지고 0값으로 초기화된 update array
w_update = np.zeros_like(w)
b_update = np.zeros_like(b)
y_pred = np.dot(x,w.T)+b # w.T: 행과열을 바꾸어준다.
diff = y-y_pred
b_factors = np.ones((N,1))
# w,b를 업데이트해준다. 손실함수을 미분한 식 (아직 완전히 업데이트된것이 아님 w = w-w_update)
w_update = -(2/N)*learning_rate*(np.dot(x.T,diff))
b_update = -(2/N)*learning_rate*(np.dot(b_factors.T,diff))
return w_update,b_update미분한 값을 구하는 함수를 만들어 주었다.

위 식과 동일한 것을 알 수 있다.
def grandient_descent_steps(x,y,iter = 1000):
# w,b를 모두 0으로 초기화
w = np.zeros((1,1))
b = np.zeros((1,1))
for ind in range(iter):
w_update,b_update = get_weight_update(w,b,x,y,learning_rate=0.01)
w = w-w_update
b = b-b_update
return w,b이제 완전히 업데이트 해주는 함수를 만들었다. iter는 모델을 학습시키는 횟수이다
w,b = grandient_descent_steps(x,y,iter = 1000)
print(w,b)
y_pred = w*x+b
print(get_cost(y,y_pred))마지막으로 업데이트된 w와b를 출력하고 get_cost함수로 차의 제곱의 평균을 구한다.
결과는 다음과 같다.
[[4.02181364]] [[6.16203122]]
0.9934784315632568
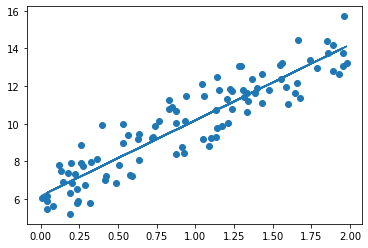
우리가 구한 직선과 산점도 분포도를 곂쳐서 보면 다음과 같다.
'파이썬 머신러닝' 카테고리의 다른 글
| [머신러닝][kaggle 실습- 보험 비용 예측하기] (2) | 2021.02.23 |
|---|---|
| [머신러닝][Deep learning을 이용한 XOR문제해결] (0) | 2021.02.14 |
| [머신러닝][Classification 알고리즘 실습-Mushroom Classification] (0) | 2021.02.14 |
| [머신러닝][코로나 확진자 예측하기] (1) | 2021.02.09 |
| Linear Regression 을 이용한 주식 가격 예측 프로그램 (0) | 2021.01.29 |